재귀(recursion)는 어떠한 이벤트에서 자기 자신을 포함하고 다시 자기 자신을 이용하여 정의되는 경우를 의미합니다. 재귀를 효과적으로 사용하면 프로그램을 간결하고 효율성 좋게 작성할 수 있습니다.
재귀를 사용하는 대표적인 예로 양의 정수 곱을 구하는 팩토리얼(factorial) 문제가 있습니다. 팩토리얼은 양의 정수를 순서대로 곱한다는 의미로 순차 곱셈이라고도 합니다. 팩토리얼 n! 의 정의(n은 양의 정수)는
1) 0!=1
2) n>0이면 n!=nx(n-1)!
#factorial.py

factoial함수는 매개변수 n에 전달받은 값이 0보다 크면 n*factorial(n-1)의 값을 반환하고, 그렇지 않으면 1을 반환합니다. 파이썬에서는 팩토리얼 값을 구하는 표준 라이브러리로 math모듈에서 factorial() 함수를 제공합니다.
옆과 같이 자기 자신의 똑같은 함수를 호출하는 방식을 직접(direct) 재귀라고 합니다. 반면에 간접(indirect) 재귀는 자신의 함수가 다른 함수를 호출하고 다시 원래의 함수를 호출하는 구조를 의미합니다.
< 유클리드 호제법 >
두 정숫값의 최대 공약수(GCD)를 재귀적으로 구하는 방법을 생각해 봅시다. 2개의 정수 값을 직사각형 두 변의 길이라고 생각하면 두 정숫값의 최대공약수를 구하는 문제는 다음과 같이 바꿀 수 있는데, 예로 변의 길이가 22와 8인 직사각형에서 정사각형을 만드는 과정을 살펴봅시다.
1) 22 X 8의 직사각형에서 짧은 변의 길이인 8을 한 변으로 하는 정사각형으로 나눕니다. 그러면 8X8크기의 정사각형 2개, 8X6 크기의 직사각형이 남습니다.
2) 남은 8X6크기의 직사각형에서도 다시 같은 과정을 수행하면 6X6크기의 정사각형 1개가 만들어지고 6X2의 직사각형이 남습니다.
3) 남은 6X2크기의 직사각형에서 같은 과정을 수행하면 2X2크기의 정사각형 3개가 만들어지고, 이렇게 얻은 정사각형의 변의 길이인 2가 8과 22의 최대 공약수입니다.
========================================================================================
위에서 두 정숫값이 주어질 때 큰 값을 작은 값으로 나누어 떨어지면 작은 값이 최대 공약수가 됩니다. 나누어 떨어지지 않으면 작은 값과 나머지에 대해 같은 과정을 나누어 떨어질 때까지 재귀적으로 반복합니다. 수학적으로 표현해보면 두 정수 x와 y의 최대 공약수를 gcd(x, y)로 표기합니다. 예로 x=az, y=bz를 만족하는 정수 a, b와 최대의 정수 z가 존재한다 했을 때 z는 gcd(x, y)라고 할 수 있습니다.
1) y가 0이면 ---> x
2) y가 0이 아니면 ---> gcd(y, x% y)
위 알고리즘을 유클리드 호제법(Euclidean algorithm)이라고 합니다.
#gcd. py

파이썬에서 최대 공약수를 구하는 표준 라이브러리로 math모듈에서 gcd() 함수를 제공합니다. 예를 들어 math.gcd(a, b)는 정수 a와 b의 최대 공약수를 반환합니다. a, b가 0이 아닌 경우 gcd(a, b)의 값은 a와 b모두를 나누어 떨어지게 하는 가장 큰 정수를 반환합니다.
< 하노이 탑 >
하노이 탑(towers of Hanoi)은 작은 원반이 위에, 큰 원반이 아래에 위치하는 규칙을 지키면서 기둥 3개를 이용해서 원반을 옮기는 문제입니다. 먼저 크기가 모두 다른 원반이 첫 번째 기둥에 쌓여있는 상태로 시작하는데 크기가 큰 순서대로 쌓여있습니다. 이 상태에서 원반 3개를 모두 세 번째 기둥에 최소 횟수로 옮기면 됩니다. 원반은 1개씩 옮길 수 있으며 큰 원반은 작은 원반 위에 쌓을 수 없다는 규칙을 지켜야 합니다.

move() 함수의 매개변수 no는 옮겨야 할 원반의 개수, x는 시작 기둥의 번호, y는 목표 기둥의 번호입니다. 옆의 프로그램에서는 기둥 번호를 정숫값 1,2,3으로 표현하고 기둥 번호의 합이 6이므로 시작 기둥, 목표 기둥이 어디 위치에 있든 중간 기둥은 (6-x-y)로 구할 수 있습니다. 맨 아래의 원반을 제외한 나머지를 중간 기둥으로 옮긴 후 가장 큰 원반을 목표 기둥 3에 놓고, 중간 기둥의 원반들을 목표 기둥에 놓는 것입니다.
< 8 퀸 문제 >
8퀸 문제(8-queen problem)는 재귀 알고리즘을 설명할 때 자주 나오는 예제로, 19세기 수학자 카를 F. 가우스가 오답을 발표한 것으로 유명합니다. 이 문제는 다음과 같은데 8개의 퀸이 서로 공격하여 잡을 수 없도록 8X8 체스판에 배치하는 것입니다.
차례로 조건을 추가하며 퀸의 배치를 생각해본다고 가정하고, 조건이 없을 때 퀸의 8개의 퀸 배치는 64x63x62..... x57= 178,462,987,637,760의 조합의 수가 만들어집니다. 하지만 퀸은 자신과 같은 열에 있는 다른 퀸을 공격할 수 있으므로 각 열에 퀸을 1개만 배치한다는 조건을 만들면 8x8x8..... x8= 16,777,216의 조합의 수가 만들어집니다.
#8 queen_b. py

옆 코드는 조합만 나열할 뿐 아직 8 퀸 문제를 해결한 것은 아닙니다. 배열 pos는 퀸의 배치를 나타내는데, i열에 배치한 퀸의 위치가 j행에 있다면, pos [i]의 값을 j로 합니다. 예를 들어 pos [0]의 값이 0이라면 퀸이 0열 0행에 배치되었다는 것을 의미하고, pos [1]의 값이 4라면 퀸은 1열 4행에 배치되어 있습니다. set()은 pos [i]에 0~7까지의 값을 차례로 대입하여 i열에 퀸을 1개만 배치하는 8가지 조합을 만다는 재귀 함수입니다. 즉 i는 퀸이 배치될 열입니다. 호출된 set()함수는 i에 0을 전달 받습니다. 여기서 실행하는 것이 0열에 퀸을 1개만 배치하는 작업입니다. for문으로 반복을 수행하여 j값을 0~7까지 1씩 증가시키면서 pos[i]에 j를 대입하여 퀸을 j행에 배치합니다. 이 대입에서 0열의 배치가 확정되므로 다음 1열의 배치가 필요합니다. 이때 수행하는 것이 18행(set(i+1))의 재귀 호출입니다. 이렇게 차례로 가지가 뻗어나가듯 배치 조합을 열거하는 방법을 분기(branching) 작업이라고 합니다.
분기 작업으로 퀸을 배치하는 조합을 나열할 수는 있지만 8 퀸 문제의 최종 답을 얻을 수는 없습니다.
각 행에 퀸을 1개만 배치합니다.라는 조건을 #8 queen_b. py에 더한 것이 아래 코드입니다.
#8 queen_bb. py

옆 코드는 열과 행에 퀸이 동시에 겹치지 않도록 조건을 추가한 코드입니다. flag라는 새로운 list형 배열을 사용하며 이 배열은 같은 행에 중복하여 퀸을 배치하지 않기 위한 표시로 사용됩니다. j행에 퀸을 배치하면 flag [j]를 True, 배치하지 않으면 False로 합니다. 0열에 퀸을 배치하기 위해 호출된 set() 함수는 for문의 동작으로 j를 0~7까지 1씩 증가시킵니다. 따라서 flag [0]이 False이므로 맨 처음에는 0행에 퀸을 배치합니다. 이때 flag [0]에 퀸의 배치를 나타내는 True를 대입하고 set() 함수를 재귀적으로 호출합니다. 호출된 set() 함수에서는 다음 1열에 퀸을 배치합니다. 또한 재귀 호출한 set(i+1) 함수가 끝나면 퀸을 j행에서 제거해야 하므로 flag [j]에 아직 배치하지 않았음을 나타내는 Fasle를 대입합니다. set() 함수에는 퀸을 아직 배치하지 않은 행에만 퀸을 배치할 수 있습니다. 이처럼 필요하지 않은 분기를 없애서 불필요한 조합을 열거하지 않는 방법을 한정(bounding) 작업이라고 합니다. 분기 작업과 한정 작업을 조합하여 문제를 풀이하는 방법을 분기 한정 법이라고 합니다.
각 행과 열에 퀸이 겹치지 않게 고려한 것에 추가로 퀸은 대각선으로 움직일 수 있기 때문에, 어떤 대각선에서 보더라도 퀸을 1개만 배치하는 한정 작업을 추가로 적용해야 합니다. 2개의 대각선의 조건을 추가하여 만들어진 프로그램이 8 queen.py입니다.
#8 queen. py
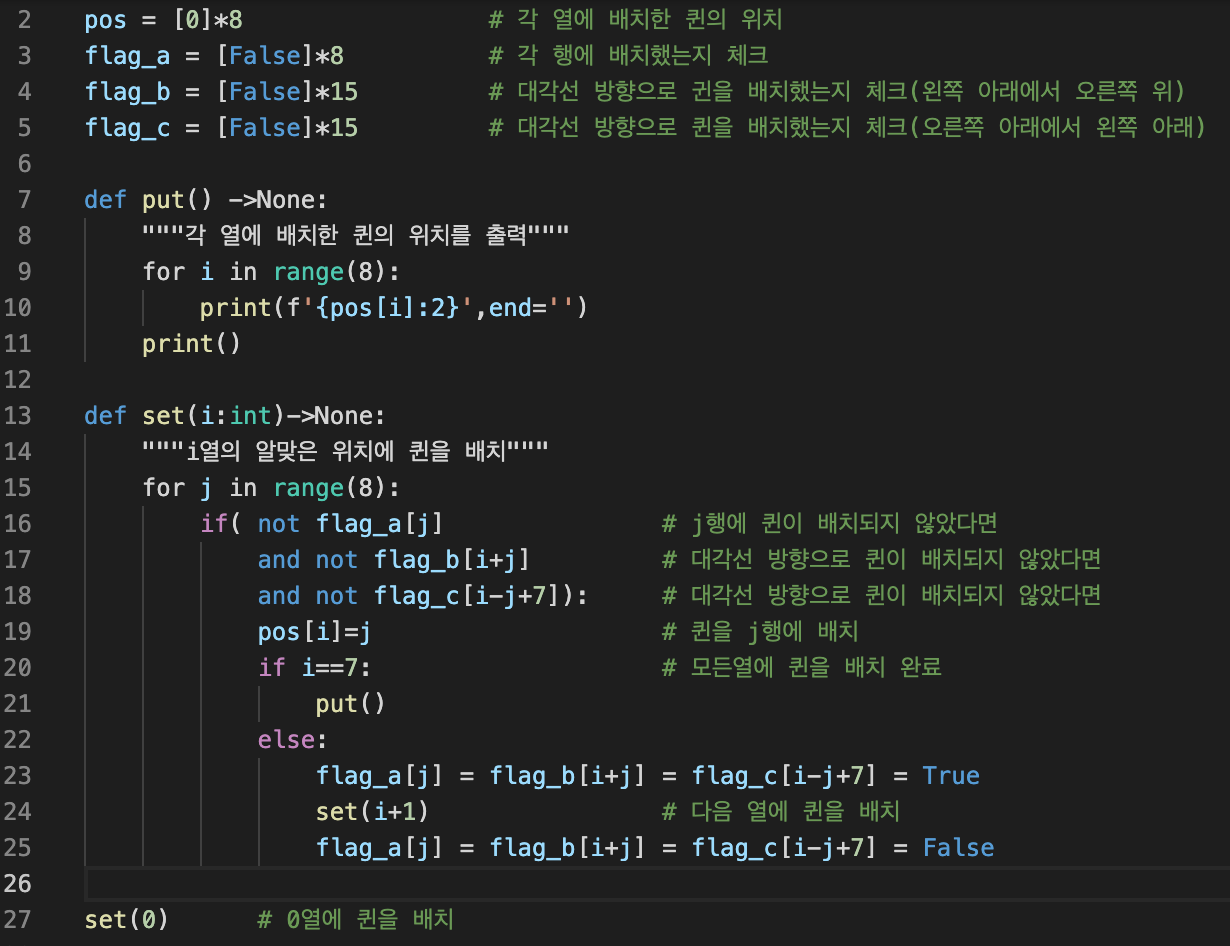
flag_b와 flag_c는 2개 방향의 대각선에 퀸을 배치했는지 검토하는 새로 추가한 배열입니다. 이제 각 칸에 배치된 퀸을 검토할 때 같은 행과 더불어 대각선으로 배치되었는지도 판단합니다.
배열 3개를 사용하는 한정 작업을 통하여 8 퀸 문제를 해결할 수 있습니다. 옆의 코드를 실행하면 92가지 조합이 출력됩니다.
'Python > Do it Python' 카테고리의 다른 글
| Python Stack,Queue (1) | 2021.08.08 |
|---|---|
| Python 검색 알고리즘 (1) | 2021.08.07 |
| Python 알고리즘 자료구조와 배열(하) (0) | 2021.07.21 |
| Python 알고리즘 자료구조와 배열(상) (1) | 2021.07.18 |
| Python 알고리즘 기초 (0) | 2021.07.15 |



